在上篇文章《如何快速开平方根?》中,我向大家演示了如何在没有计算器的情况下,快速手算平方根。写完上篇文章之后我就在想,能不能把之前的方法推广到手算立方根?
这篇文章我们就来探索如何快速手算立方根。
在开始尝试之前,我先介绍一个公式:
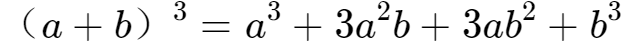
。
有了这个公式,我们就可以开始尝试了,这里我用
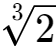
、
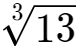
进行尝试。
一、
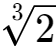
如何快速开立方根?
我们先把
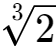
的实际数值展示出来,以便后面作对比:
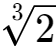
=1.25992……
1、首先
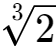
在1和2之间,我们可以假设
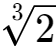
=1+a,这里a是1个比1小的数字。
2、等式两边同时立方,可得:
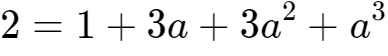
。
3、因为a<1,所以
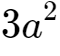
、
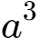
是一个比较小的数,我们可以将它们忽略掉。
4、等式就变为:2=1+3a,于是
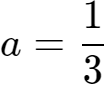
。
5、
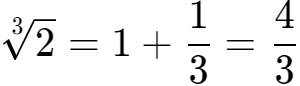
=1.33……=1.3。(取1位小数)
(这时1.3与
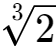
=1.25992……在小数点后第1位数上已知较为接近了)
6、如果想让结果精确些,我们可以用上面的方法重复一次。
7、再假设
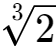
=1.3+b,这里b是1个比1小的数字。
8、等式两边同时立方,可得:2=
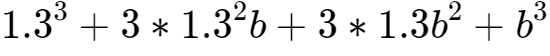
。
9、因为b<1,所以
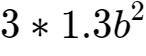
、
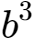
是一个比较小的数,我们可以将它们忽略掉。
10、等式就变为:
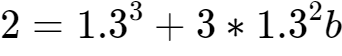
,于是b=-0.03886……。
11、
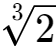
=1.3+b=1.3-0.03886……=1.26114……=1.26。(取2位小数)
(这时1.26与
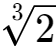
=1.25992……在小数点后第2位数上已知较接近了)
12、如果想让结果再精确些,我们再重复上面的方法一次。
13、再假设
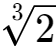
=1.26+c,这里c是1个比1小的数字。
14、等式两边同时立方,可得:
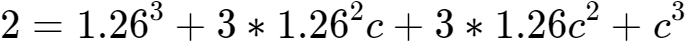
。
15、因为c<1,所以
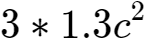
、
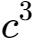
是一个比较小的数,我们可以将它们忽略掉。
16、等式就变为:
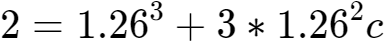
,于是c=-0.0000789……。
17、
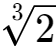
=1.26+c=1.3-0.0000789……=1.259921……=1.260。(取3位小数)
(这时1.260与
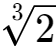
=1.25992……就非常接近了,如果我们大胆一点,取1.259921……小数点后5位数,得到的数值1.25992就与
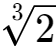
=1.25992……是一致的)
二、
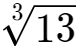
如何快速开立方根?
我们先把
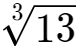
的实际数值展示出来,以便后面作对比:
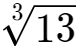
=2.351334……
1、首先
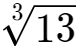
在2和3之间,我们可以假设
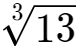
=2+a,这里a是1个比1小的数字。
2、等式两边同时立方,可得:
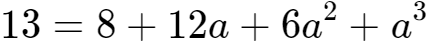
。
3、因为a<1,所以
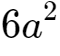
、
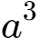
是一个比较小的数,我们可以将它们忽略掉。
4、等式就变为:13=8+12a,于是
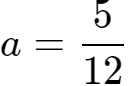
。
5、
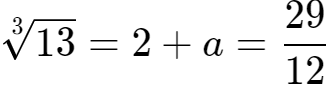
=2.41……=2.4。(取1位小数)
(这时2.4与
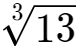
=2.351334……在小数点后第1位数上已知较为接近了)
6、如果想让结果精确些,我们可以用上面的方法重复一次。
7、再假设
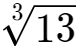
=2.4+b,这里b是1个比1小的数字。
8、等式两边同时立方,可得:

。
9、因为b<1,所以
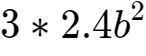
、
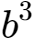
是一个比较小的数,我们可以将它们忽略掉。
10、等式就变为:
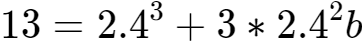
,于是b=-0.047685……。
11、
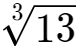
=2.4+b=2.4-0.047685……=2.35231……=2.35。(取2位小数)
(这时2.35与
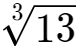
=2.351334……在小数点后第2位数上已知较接近了)
12、如果想让结果再精确些,我们再次重复上面的方法一次。
13、再假设
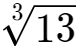
=2.35+c,这里c是1个比1小的数字。
14、等式两边同时立方,可得:
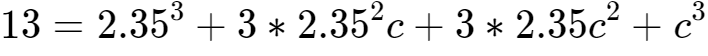
。
15、因为c<1,所以
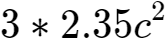
、
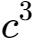
是一个比较小的数,我们可以将它们忽略掉。
16、等式就变为:
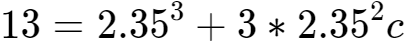
,于是c=0.001335446……。
17、
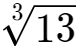
=2.35+c=2.35+0.001335446……=2.351335446……=2.351。(取3位小数)
(这时2.351与
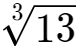
=2.351334……在小数点后第3位数上已知较接近了,如果我们大胆一点,取2.351335446……小数点后5位数,得到的数值2.35133就与
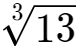
=2.351334……是一致的)
上面的方法,我们还可以进一步推广,用来开4次方根、5次方根、6次方根……
我是科学发现之历程,一个致力于科普数学、物理的科技媒体。想了解更多相关的知识,关注微信公众号科学发现之历程,期待你的到来~







