已知三角形两直角边求第三边,怎么求 （在已知三角形两个直角边的前提下，如何求得第三个边的数值）

一、勾股定理

1.勾股定理：如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么

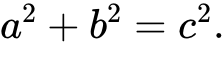
2.勾股定理的证明方法：通过剪拼，借助面积进行证明。

3.勾股定理的应用条件：只适用于直角三角形，所以常作辅助线——高，构造直角三角形。

4.勾股定理的应用

（1）已知直角三角形的两边，求第三边；

（2）表示长度为无理数的线段；

（3）在数轴上作出表示无理数的点。

二、勾股定理的逆定理

1.勾股定理的逆定理

如果三角形的三边长a，b，c满足条件

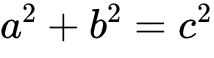
，那么这个三角形是直角三角形。

（1）若a，b，c是一组勾股数，那么ak，bk，ck（k是正整数）也是一组勾股数。

（2）若a，b，c是一直角三角形的三边长，则以ma，mb，mc（m>0）为三边的三角形也是直角三角形。

2.互逆命题

如果两个命题的题设、结论正好相反，这样的两个命题叫做互逆命题。

3.逆定理：如果一个定理的逆命题经过证明是正确的，它也是一个定理，称这两个定理互为逆定理。